Jan 21, 2014
You drop a ball. You drop a key. You drop a piece of lead. They each slip from your hand and tumble to the ground. But you have an orderly mind (you're a physicist) and, to you, falling things don't seem haphazard — they seem neat. The unruly world has rules, laws. So instead of saying "Bummer!" you say, "Of course! How beautiful! How logical!"
Galileo thought this way. He got a bunch of weights, dropped them and discovered just such a rule. (I would never have expected it. When I drop an object, it feels like a drama, a short story that will never repeat the same way. But I'm not a physicist — I am whatever the opposite of a physicist is.)
Here's what Galileo did. (You can do it, too. In his new book, The Accidental Universe, physicist Alan Lightman tells us how.)
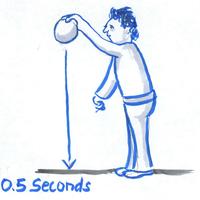
First, "drop a weight to the floor from a height of 4 feet, and time the duration of its fall," Alan says:

Robert Krulwich/NPR
You should get about 0.5 seconds.
Then try it again, this time from a height of 8 feet. That should take, Alan says, about 0.7 seconds:

Robert Krulwich/NPR
Again — but now from a height of 16 feet. Duration: about 1 second.

Robert Krulwich/NPR
Says Alan: "Repeat [this experiment] from several more heights and you will discover the rule that the time exactly doubles with every quadrupling of height."
This always happens. Four times higher, the falling time doubles. Always. "With this rule," says Alan, you can now predict the time to fall from any height. You have witnessed, firsthand," he says triumphantly, "the lawfulness of nature." As you watch things drop, now you can say, "Of course. How beautiful! How logical!"
Mathematicians believe (actually, they know) that there are rules out there in the real world — patterns that don't vary. If you follow the math, the equations can lead you to otherwise invisible objects in the universe, things that logic tells you must be there. The math says, "Look here." You look, and bingo! There it is. (That's how we found the planet Uranus.)
But sometimes the math does something even stranger. Spookier. Instead of "Of course!" it makes you say, "Huh?" (Or, in less polite circles, "WTF?")
What you're about to see is a deeply beautiful "Huh?" story.
This Is A Queer Universe, Says The Math
The math isn't hard. It comes in simple steps. But it leads to the strangest, most impossible-sounding conclusion. Yet every step you take makes perfect sense until you get to the end — and go, "No way!"
I'm a total math dummy, and yet I followed this puzzle almost to the end. It's one of the few times I've ever been able to feel what it's like to be a mathematician exploring the universe.
Go ahead. Even if you think you'll hate it, take the chance. It's only a few minutes long. Give yourself a "Huh?"